Primero vayamos al grano.


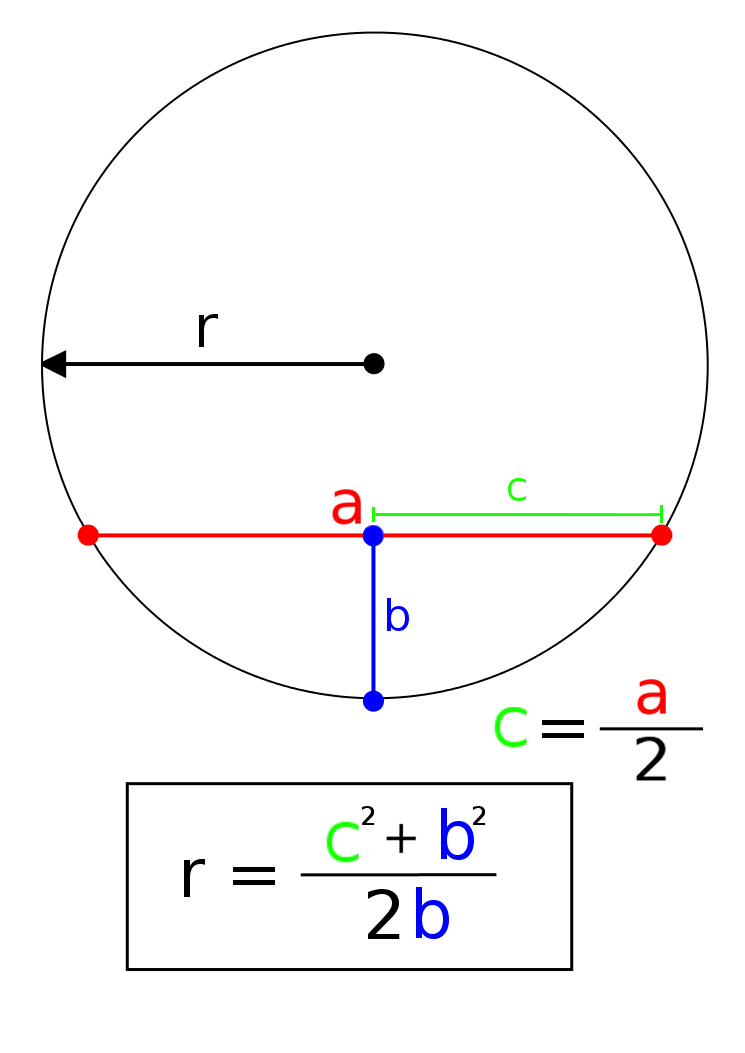
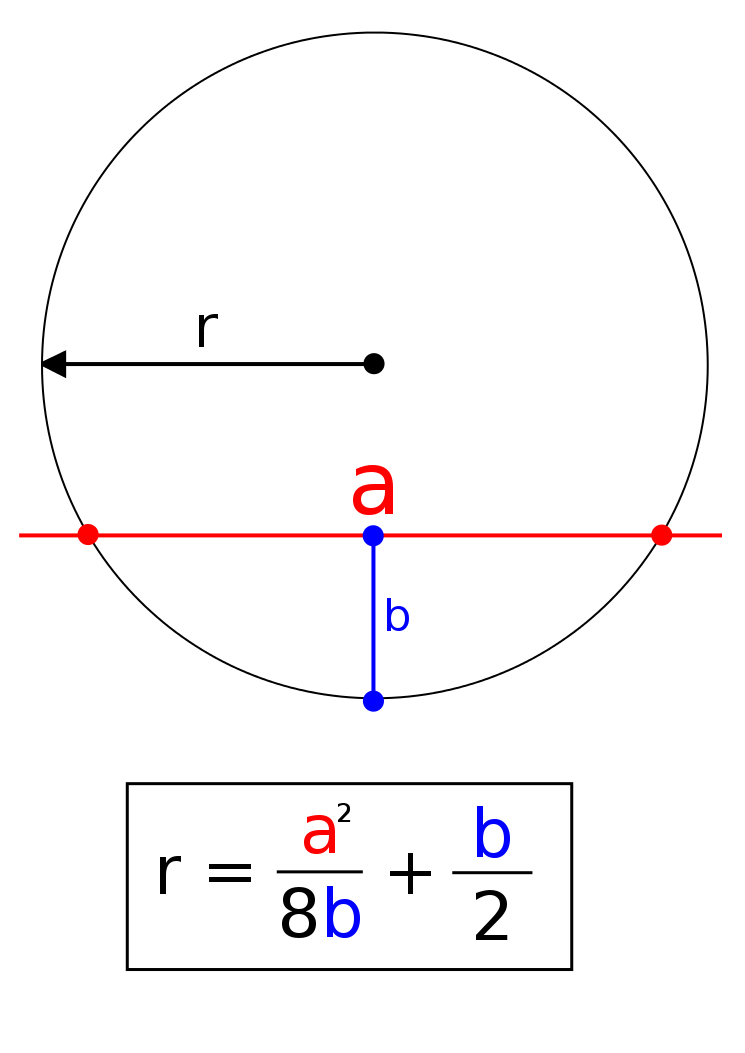
a es la distancia entre cada intersección que
hay entre la circunferencia y la secante.
Y b es la distancia perpendicular de la secante hasta
una tangente
paralela a ella. (hay varias formas de definir a
b)
Hace mucho tiempo me tocó deducir esta formula porque nunca la logré conseguir por internet (aunque a la final nunca hizo falta jeje).
Lo que me motivó a deducirla era que hacia falta fabricar unos álabes de un impulsor que tenian una ligera curvatura cóncava, y debido a la falta de planos, tocaba copiar la muestra y necesitaba calcular ese radio de curvatura, y asi es que se me ocurrió esta idea de medir la longitud de una regla o un palo recto (a), ponerlo paralelo a la direccion de la curvatura, para luego medir desde el centro del palo perpendicularmente hasta el fondo de la pieza (b), y así con solo esos dos datos poder calcular el radio de curvatura.
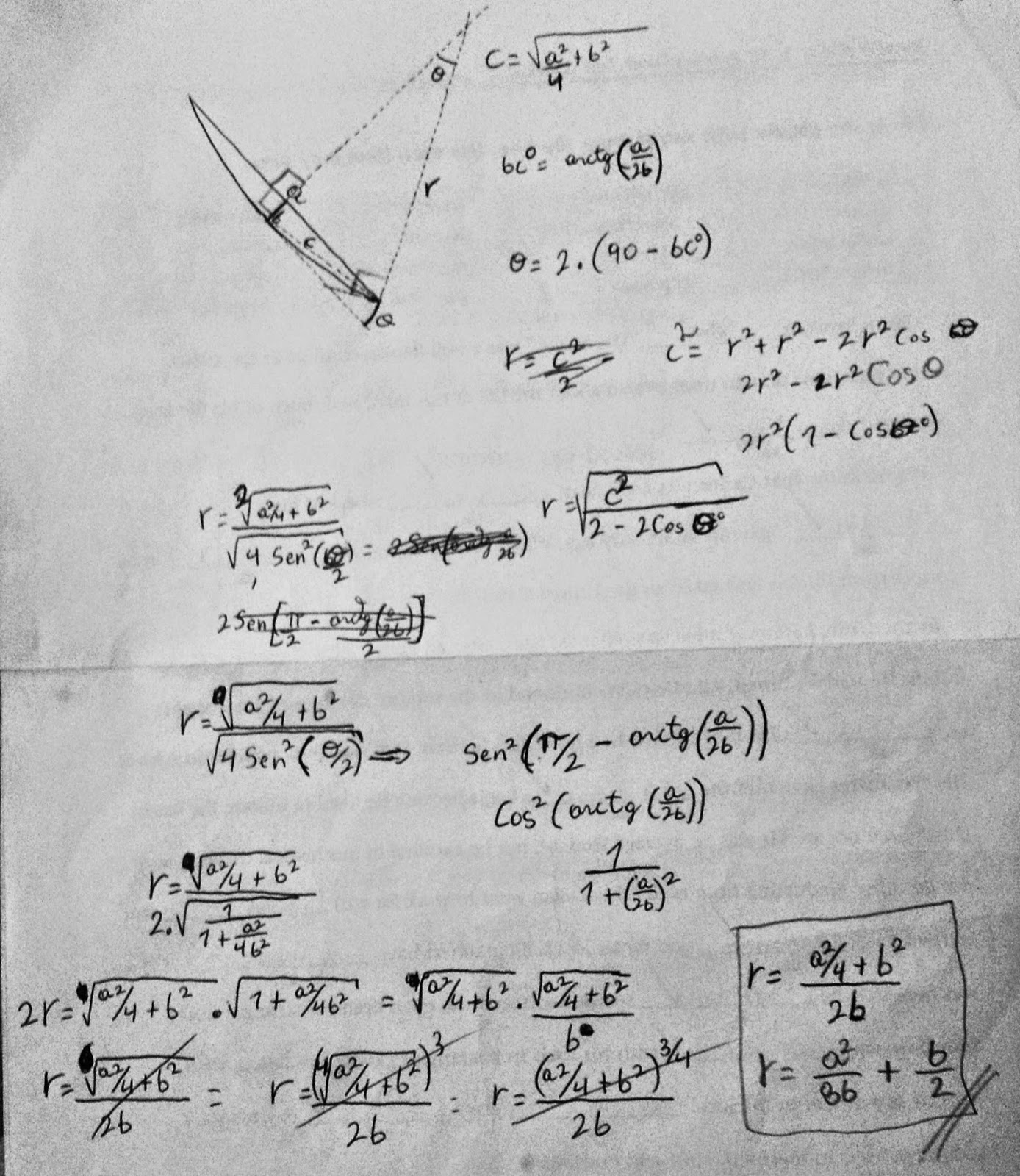
Este es el borrador en donde hice las deducciones, pero les advierto que está muy desorganizado y con tachaduras.